import numpy as np
from scipy.interpolate import interp1d
import scipy
from matplotlib import pyplot as plt
import IPython.display as ipd
from IPython.display import Image
import librosa
from utils import *3.5. 디지털 신호
Digital Signals
오디오 신호(signal)의 디지털화에 필요한 샘플링(sampling)과 양자화(quantization)에 대해 소개하며, 또한 간섭(interference) 및 비팅(beating) 현상을 다룬다.
이 글은 FMP(Fundamentals of Music Processing) Notebooks을 참고로 합니다.
디지털 신호 샘플링 (Sampling)
- 아날로그 신호는 시간과 진폭 모두에서 연속적인 범위의 값을 가지므로 일반적으로 무한한 수의 값이 생성된다. 컴퓨터는 한정된 수의 값만 저장하고 처리할 수 있기 때문에 파형을 이산 표현, 즉 일반적으로 디지털화라고 하는 프로세스로 변환해야 한다. 오디오 신호를 디지털화하는 가장 일반적인 접근 방식은 샘플링(sampling) 및 양자화(quantization) 라는 두 단계로 구성된다.
샘플링(Sampling)
신호 처리(signal processing)에서, 샘플링이란 연속 신호를 시간 축의 이산적 부분집합으로만 정의된 이산 신호로 축소시키는 것을 말한다.
적절한 인코딩을 통해 이산 집합이 정수 집합 \(\mathbb{Z}\)의 하위 집합 \(I\)라고 가정하고는 한다. 그런 다음 이산시간(discrete time, DT)-신호는 함수 \(x\colon I\to\mathbb{R}\)로 정의되며 여기서 도메인 \(I\)는 시점에 해당한다.
\(\mathbb{Z}\setminus I\)의 포인트에 대해 모든 값을 0으로 설정하는 것만으로 도메인 \(I\)에서 도메인 \(\mathbb{Z}\)로 모든 DT 신호를 확장할 수 있으므로 \(I=\mathbb{Z}\)를 가정할 수 있다.
연속시간(continuous time, CT)-신호 \(f\colon\mathbb{R}\to\mathbb{R}\)를 DT-신호 \(x\colon\mathbb{Z}\to\mathbb{R}\)로 변환하는 가장 일반적인 샘플링 절차는 등거리 샘플링(equidistant sampling)이라고 한다.
양의 실수 \(T>0\)를 고정하면, DT-신호 \(x\)는 다음과 같이 설정하여 얻는다.
- \(x(n):= f(n \cdot T)\) for \(n\in\mathbb{Z}\)
\(x(n)\) 값은 원래 아날로그 신호 \(f\)의 시간 \(t=n\cdot T\)에서 가져온 샘플이라고 한다. 간단히 말해서 이 절차를 \(T\)-샘플링 이라고도 한다.
숫자 \(T\)는 샘플링 주기 (sampling period) 라고 하고 역(inverse) \(F_\mathrm{s}:=1/T\)는 샘플링 레이트/속도 (sampling rate) 라고 한다. 샘플링 레이트는 초당 샘플 수를 지정하며 헤르츠(Hz) 단위로 측정된다.
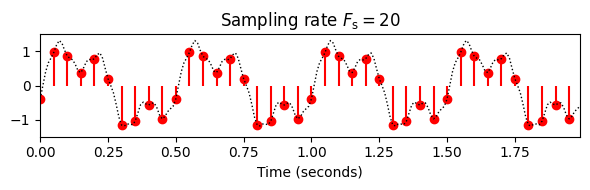
다음 코드 셀에서 높은 샘플링 속도로 샘플링된 DT-신호의 선형 보간법을 통해 정의된 CT-신호 \(f\)로 시작한다. 그림에서 이 CT-신호는 검은색 곡선으로 표시된다. 등거리 샘플링을 적용하여 빨간색 줄기 플롯으로 시각화된 DT 신호 \(x\)를 얻는다.
def generate_function(Fs, dur=1):
"""Generate example function
Args:
Fs (scalar): Sampling rate
dur (float): Duration (in seconds) of signal to be generated (Default value = 1)
Returns:
x (np.ndarray): Signal
t (np.ndarray): Time axis (in seconds)
"""
N = int(Fs * dur)
t = np.arange(N) / Fs
x = 1 * np.sin(2 * np.pi * (2 * t - 0))
x += 0.5 * np.sin(2 * np.pi * (6 * t - 0.1))
x += 0.1 * np.sin(2 * np.pi * (20 * t - 0.2))
return x, t
def sampling_equidistant(x_1, t_1, Fs_2, dur=None):
"""Equidistant sampling of interpolated signal
Args:
x_1 (np.ndarray): Signal to be interpolated and sampled
t_1 (np.ndarray): Time axis (in seconds) of x_1
Fs_2 (scalar): Sampling rate used for equidistant sampling
dur (float): Duration (in seconds) of sampled signal (Default value = None)
Returns:
x (np.ndarray): Sampled signal
t (np.ndarray): Time axis (in seconds) of sampled signal
"""
if dur is None:
dur = len(t_1) * t_1[1]
N = int(Fs_2 * dur)
t_2 = np.arange(N) / Fs_2
x_2 = interp1d(t_1, x_1, kind='linear', fill_value='extrapolate')(t_2)
return x_2, t_2Fs_1 = 100
x_1, t_1 = generate_function(Fs=Fs_1, dur=2)
Fs_2 = 20
x_2, t_2 = sampling_equidistant(x_1, t_1, Fs_2)
plt.figure(figsize=(6, 2))
plt.plot(t_1, x_1, 'k')
plt.title('Original CT-signal')
plt.xlabel('Time (seconds)')
plt.ylim([-1.5, 1.5])
plt.xlim([t_1[0], t_1[-1]])
plt.tight_layout()
plt.figure(figsize=(6, 2))
plt.stem(t_2, x_2, linefmt='r', markerfmt='ro', basefmt='None')
plt.plot(t_1, x_1, 'k', linewidth=1, linestyle='dotted')
plt.title(r'Sampling rate $F_\mathrm{s} = %.0f$'%Fs_2)
plt.xlabel('Time (seconds)')
plt.ylim([-1.5, 1.5])
plt.xlim([t_1[0], t_1[-1]])
plt.tight_layout()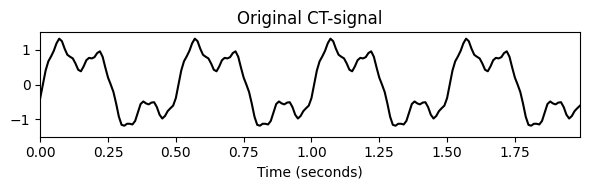
에일리어싱 (Aliasing)
또는 위신호현상
일반적으로 샘플링은 처리 과정에서 정보가 손실되고 원본 CT-신호를 샘플링된 버전으로부터 복구할 수 없다는 점에서 손실적인(lossy) 작업이다.
CT-신호에 주파수 스펙트럼 측면(대역 제한(bandlimited) 필요)에서 추가 속성이 있는 경우에만 완벽한 재구성이 가능하다. 이것이 유명한 샘플링 정리(sampling theorem)의 주장이다. 샘플링 이론은 또한 DT-신호의 샘플에 의해 가중된 적절하게 이동된 \(\mathrm{sinc}\)-함수를 중첩하여 원래 CT-신호가 어떻게 재구성될 수 있는지 보여준다.
추가적인 속성이 없다면 샘플링으로 인해 신호의 특정 주파수 구성 요소를 구분할 수 없게 되는 에일리어싱(aliasing)이라는 현상이 발생할 수 있다.
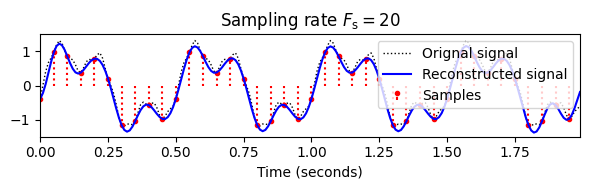
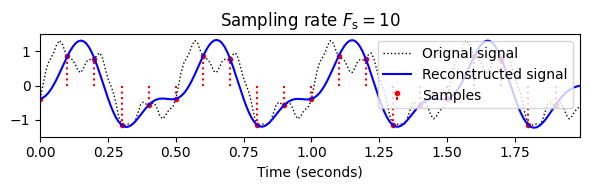
이 효과는 다음 그림에 설명되어 있다. 높은 샘플링 속도를 사용하면 원본 CT-신호를 높은 정확도로 재구성할 수 있다. 그러나 샘플링 속도를 낮추면 더 높은 주파수 구성 요소가 잘 캡처되지 않고 원래 신호의 대략적인 근사치만 남는다.
def reconstruction_sinc(x, t, t_sinc):
"""Reconstruction from sampled signal using sinc-functions
Args:
x (np.ndarray): Sampled signal
t (np.ndarray): Equidistant discrete time axis (in seconds) of x
t_sinc (np.ndarray): Equidistant discrete time axis (in seconds) of signal to be reconstructed
Returns:
x_sinc (np.ndarray): Reconstructed signal having time axis t_sinc
"""
Fs = 1 / t[1]
x_sinc = np.zeros(len(t_sinc))
for n in range(0, len(t)):
x_sinc += x[n] * np.sinc(Fs * t_sinc - n)
return x_sinc
def plot_signal_reconstructed(t_1, x_1, t_2, x_2, t_sinc, x_sinc):
plt.figure(figsize=(6, 2))
plt.plot(t_1, x_1, 'k', linewidth=1, linestyle='dotted', label='Orignal signal')
plt.stem(t_2, x_2, linefmt='r:', markerfmt='r.', basefmt='None', label='Samples')
plt.plot(t_1, x_sinc, 'b', label='Reconstructed signal')
plt.title(r'Sampling rate $F_\mathrm{s} = %.0f$'%(1/t_2[1]))
plt.xlabel('Time (seconds)')
plt.ylim([-1.5, 1.5])
plt.xlim([t_1[0], t_1[-1]])
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()Fs_2 = 40
x_2, t_2 = sampling_equidistant(x_1, t_1, Fs_2)
t_sinc = t_1
x_sinc = reconstruction_sinc(x_2, t_2, t_sinc)
plot_signal_reconstructed(t_1, x_1, t_2, x_2, t_sinc, x_sinc);
Fs_2 = 20
x_2, t_2 = sampling_equidistant(x_1, t_1, Fs_2)
t_sinc = t_1
x_sinc = reconstruction_sinc(x_2, t_2, t_sinc)
plot_signal_reconstructed(t_1, x_1, t_2, x_2, t_sinc, x_sinc);
Fs_2 = 10
x_2, t_2 = sampling_equidistant(x_1, t_1, Fs_2)
t_sinc = t_1
x_sinc = reconstruction_sinc(x_2, t_2, t_sinc)
plot_signal_reconstructed(t_1, x_1, t_2, x_2, t_sinc, x_sinc);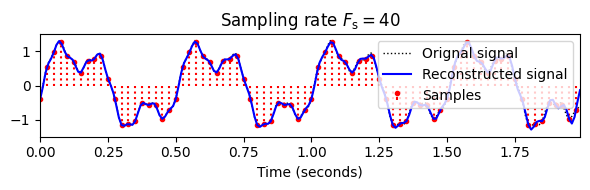
- 다음 예는 에일리어싱이 음질에 미치는 영향을 나타낸다. 높은 샘플링 속도(\(F_s=8192Hz\))의 음악 신호로 시작한 다음 두배씩 줄여나가보자.
x, Fs = librosa.load('../audio/piano_c_scale.wav', sr=8000)
Fs_orig = Fs
len_orig = len(x)
for i in range(5):
print('Sampling rate Fs = %s; Number of samples = %s' % (Fs, len(x)))
x_play = scipy.signal.resample(x, len_orig)
ipd.display(ipd.Audio(data=x_play, rate=Fs_orig))
Fs = Fs // 2
x = x[::2]Sampling rate Fs = 8000; Number of samples = 54001Sampling rate Fs = 4000; Number of samples = 27001Sampling rate Fs = 2000; Number of samples = 13501Sampling rate Fs = 1000; Number of samples = 6751Sampling rate Fs = 500; Number of samples = 3376샘플링 정리 (Sampling Theorem)
샘플링 정리 (sampling theorem)는 대역 제한이 있는(bandlimited) 연속 시간(CT) 신호를 특정 조건에서 완벽하게 재구성할 수 있다고 말한다.
보다 정확하게는 \(|\omega|>\Omega\) 에 대해 푸리에 변환 \(\hat{f}\)가 사라지면 CT 신호 \(f\in L^2(\mathbb{R})\)를 \(\Omega\)-bandlimited 라고 한다 (즉, \(\hat{f}(\omega) = 0\) for \(|\omega|>\Omega\)).
\(f\in L^2(\mathbb{R})\)를 \(\Omega\)-bandlimited 함수라고 하고, \(x\)를 \(f\)의 (with \(T:=1/(2\Omega)\)) \(T\)-샘플 버전이라고 하자 (즉, \(x(n)=f(nT)\), \(n\in\mathbb{Z}\)).
그러면 \(f\)는 다음과 같이 \(x\)로부터 재구성될 수 있다.
\[ f(t)=\sum_{n\in\mathbb{Z}}x(n)\mathrm{sinc}\left(\frac{t-nT}{T}\right) =\sum_{n\in\mathbb{Z}}f\left(\frac{n}{2\Omega}\right) \mathrm{sinc}\left(2\Omega t-n\right), \]
where the \(\mathrm{sinc}\)-function is defined as
\[\begin{equation} \mathrm{sinc}(t):=\left\{\begin{array}{ll} \frac{\sin \pi t}{\pi t},&\mbox{ if $t\not= 0$,}\\ 1,&\mbox{ if $t= 0$.} \end{array}\right. \end{equation}\]
- 즉, 대역 제한이 샘플링 속도의 절반 이하인 경우, 등거리 샘플링으로 얻은 DT 신호에서 CT 신호 \(f\)를 완벽하게 재구성할 수 있다.
- \(\mathrm{sinc}\) 함수를 기반으로 한 이 재구성은
reconstruction_sinc함수에서 사용되었다.
디지털 신호 양자화 (Quantization)
이산화 (Discretization)
위에서 연속-시간 축을 이산-시간 축으로 변환하는 과정으로서의 샘플링을 보았다. 이것은 아날로그-to-디지털의 첫번째 단계였다.
두 번째 단계에서는 가능한 진폭(amplitude)의 연속 범위(\(\mathbb{R}\)로 인코딩됨)를 가능한 값의 이산 범위(이산 집합 \(\Gamma\subset \mathbb{R}\)로 인코딩됨)로 대체해야 한다. 이 프로세스를 일반적으로 양자화(quantization) 라고 한다.
Image('../img/3.fourier_analysis/f.2.13.PNG', width=500)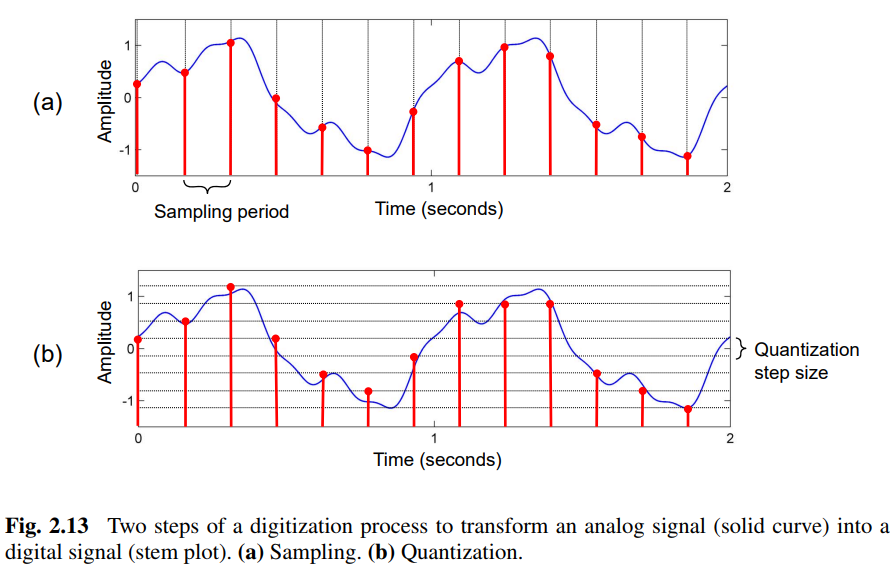
균일(Uniform) 양자화
양자화는 각 진폭 값 \(a\in\mathbb{R}\)에 값 \(Q(a)\in\Gamma\)을 할당하는 quantizer라고 하는 함수 \(Q:\mathbb{R}\to\Gamma\)로 모델링할 수 있다.
사용되는 많은 quantizer는 단순히 아날로그 값을 일부 정밀도 단위로 반올림하거나 자른다(truncate). 예를 들어 어떤 값 \(\Delta\)와 동일한 quantization step size를 갖는 일반적인 uniform quantizer는 양자화 수준을 균일하게 배치한다.
- \(Q(a) := \mathrm{sgn}(a) \cdot \Delta \cdot \left\lfloor \frac{|a|}{\Delta} + \frac{1}{2} \right\rfloor\) for \(a\in\mathbb{R}\),
- \(\mathrm{sgn}(\cdot)\)는 실수의 부호를 생성하는 signum 함수이며, 대괄호 \(\lfloor \cdot \rfloor\)는 실수를 잘라(truncate) 이 숫자 아래에서 가장 큰 정수를 생성하는 것이다.
- \(\Delta=1\)의 경우 quantizer \(Q\)는 가장 가까운 정수로 간단히 반올림된다.
양자화 오류 (Quantization Error)
샘플링과 마찬가지로 양자화는 일반적으로 손실이 많은 작업이다. 다른 아날로그 값이 동일한 디지털 값에 매핑될 수 있기 때문이다. 실제 아날로그 값과 양자화된 값의 차이를 양자화 오류라고 한다.
양자화 step size \(\Delta\)를 줄이면 일반적으로 양자화 오류가 더 작아진다. 그러나 동시에 양자화된 값의 수(따라서 이러한 값을 인코딩하는 데 필요한 비트 수)도 증가한다.
예를 들어 양자화 단계 크기 \(\Delta=1/3\)가 사용되면 주어진 신호에 대해 \(8\)의 서로 다른 양자화 값이 생성된다. 따라서 \(3\) 비트 코딩 방식을 사용하여 양자화된 값을 나타낼 수 있다. CD 녹음의 경우 \(65536\) 가능한 값을 표현할 수 있는 \(16\) 비트 코딩 체계가 사용된다.
균일 양자화 구현
- 다음에서 모든 아날로그 값이 \(s,t\in\mathbb{R}\)에 대해 \([s,t]\) 범위 내에 있다고 가정한다. 또한 여러 양자화 수준이 \(\lambda\in\mathbb{N}\)인 경우, 양자화 step size를 \(\Delta=|t-s|/(\lambda-1)\)로 정의한다. 이는 \(\lambda\) 양자화 레벨로 구성되는 (\(s\) 값으로 시작하여 \(t\) 값으로 끝남), 값 \(s\)와 \(t\) 사이의 uniform 양자화로 정의한다.
- 예를 들어 파형 기반 오디오 신호는 일반적으로 \([-1,1]\) 범위에 있다.
- \(s=-1\), \(t=1\) 및 \(\lambda=9\)의 경우 결과는 \(\Delta=1/4\)이다. 이 경우 결과 양자화 오류는 최대 1/8입니다. 다음 코드 셀에서 서로 다른 매개변수 \(s\), \(t\) 및 \(\lambda\)에 대해 균일한 양자화를 산출하는
quantize_uniform함수를 정의해보자.
def quantize_uniform(x, quant_min=-1.0, quant_max=1.0, quant_level=5):
"""Uniform quantization approach
Args:
x (np.ndarray): Original signal
quant_min (float): Minimum quantization level (Default value = -1.0)
quant_max (float): Maximum quantization level (Default value = 1.0)
quant_level (int): Number of quantization levels (Default value = 5)
Returns:
x_quant (np.ndarray): Quantized signal
"""
x_normalize = (x-quant_min) * (quant_level-1) / (quant_max-quant_min)
x_normalize[x_normalize > quant_level - 1] = quant_level - 1
x_normalize[x_normalize < 0] = 0
x_normalize_quant = np.around(x_normalize)
x_quant = (x_normalize_quant) * (quant_max-quant_min) / (quant_level-1) + quant_min
return x_quant
def plot_graph_quant_function(ax, quant_min=-1.0, quant_max=1.0, quant_level=256, mu=255.0, quant='uniform'):
"""Helper function for plotting a graph of quantization function and quantization error
Args:
ax (mpl.axes.Axes): Axis
quant_min (float): Minimum quantization level (Default value = -1.0)
quant_max (float): Maximum quantization level (Default value = 1.0)
quant_level (int): Number of quantization levels (Default value = 256)
mu (float): Encoding parameter (Default value = 255.0)
quant (str): Type of quantization (Default value = 'uniform')
"""
x = np.linspace(quant_min, quant_max, 1000)
if quant == 'uniform':
x_quant = quantize_uniform(x, quant_min=quant_min, quant_max=quant_max, quant_level=quant_level)
quant_stepsize = (quant_max - quant_min) / (quant_level-1)
title = r'$\lambda = %d, \Delta=%0.2f$' % (quant_level, quant_stepsize)
if quant == 'nonuniform':
x_quant = quantize_nonuniform_mu(x, mu=mu, quant_level=quant_level)
title = r'$\lambda = %d, \mu=%0.1f$' % (quant_level, mu)
error = np.abs(x_quant - x)
ax.plot(x, x, color='k', label='Original amplitude')
ax.plot(x, x_quant, color='b', label='Quantized amplitude')
ax.plot(x, error, 'r--', label='Quantization error')
ax.set_title(title)
ax.set_xlabel('Amplitude')
ax.set_ylabel('Quantized amplitude/error')
ax.set_xlim([quant_min, quant_max])
ax.set_ylim([quant_min, quant_max])
ax.grid('on')
ax.legend()plt.figure(figsize=(12,4))
ax = plt.subplot(1, 3, 1)
plot_graph_quant_function(ax, quant_min=-1, quant_max=4, quant_level=3)
ax = plt.subplot(1, 3, 2)
plot_graph_quant_function(ax, quant_min=-2, quant_max=2, quant_level=4)
ax = plt.subplot(1, 3, 3)
plot_graph_quant_function(ax, quant_min=-1, quant_max=1, quant_level=9)
plt.tight_layout()
plt.show()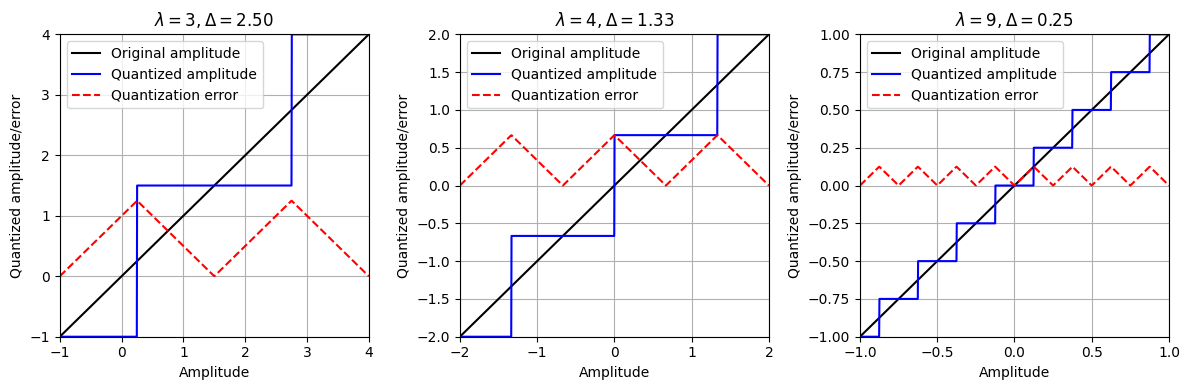
- 다음 코드 셀에서는 정현파를 신호로 사용하여 다양한 파라미터 설정에 대한 균일(uniform) 양자화 결과를 본다.
def generate_sinusoid(dur=5, Fs=1000, amp=1, freq=1, phase=0):
"""Generation of sinusoid
2.3.Audio_Represenation에 쓰인 바 있음
Args:
dur (float): Duration (in seconds) (Default value = 5)
Fs (scalar): Sampling rate (Default value = 1000)
amp (float): Amplitude of sinusoid (Default value = 1)
freq (float): Frequency of sinusoid (Default value = 1)
phase (float): Phase of sinusoid (Default value = 0)
Returns:
x (np.ndarray): Signal
t (np.ndarray): Time axis (in seconds)
"""
num_samples = int(Fs * dur)
t = np.arange(num_samples) / Fs
x = amp * np.sin(2*np.pi*(freq*t-phase))
return x, t
def plot_signal_quant(x, t, x_quant, figsize=(6, 2), xlim=None, ylim=None, title=''):
"""Helper function for plotting a signal and its quantized version
Args:
x: Original Signal
t: Time
x_quant: Quantized signal
figsize: Figure size (Default value = (8, 2))
xlim: Limits for x-axis (Default value = None)
ylim: Limits for y-axis (Default value = None)
title: Title of figure (Default value = '')
"""
plt.figure(figsize=figsize)
plt.plot(t, x, color='gray', linewidth=1.0, linestyle='-', label='Original signal')
plt.plot(t, x_quant, color='red', linewidth=2.0, linestyle='-', label='Quantized signal')
if xlim is None:
plt.xlim([0, t[-1]])
else:
plt.xlim(xlim)
if ylim is not None:
plt.ylim(ylim)
plt.xlabel('Time (seconds)')
plt.ylabel('Amplitude')
plt.title(title)
plt.legend(loc='upper right', framealpha=1)
plt.tight_layout()
plt.show()dur = 5
x, t = generate_sinusoid(dur=dur, Fs=1000, amp=1, freq=1, phase=0.0)
quant_min = -1
quant_max = 1
quant_level = 5
x_quant = quantize_uniform(x, quant_min=quant_min, quant_max=quant_max,
quant_level=quant_level)
plot_signal_quant(x, t, x_quant, xlim=[0, dur], ylim=[-1.3,1.3],
title=r'Uniform quantization with min=$%0.1f$, max=$%0.1f$, $\lambda$=$%d$'%(quant_min, quant_max, quant_level));
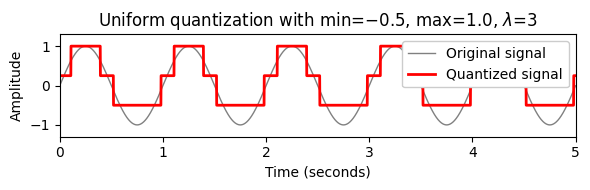
quant_min = -0.5
quant_max = 1
quant_level = 3
x_quant = quantize_uniform(x, quant_min=quant_min, quant_max=quant_max,
quant_level=quant_level)
plot_signal_quant(x, t, x_quant, xlim=[0, dur], ylim=[-1.3,1.3],
title=r'Uniform quantization with min=$%0.1f$, max=$%0.1f$, $\lambda$=$%d$'%(quant_min, quant_max, quant_level));
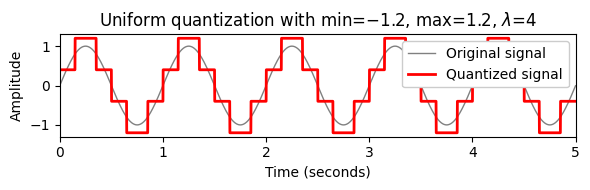
quant_min = -1.2
quant_max = 1.2
quant_level = 4
x_quant = quantize_uniform(x, quant_min=quant_min, quant_max=quant_max,
quant_level=quant_level)
plot_signal_quant(x, t, x_quant, xlim=[0, dur], ylim=[-1.3,1.3],
title=r'Uniform quantization with min=$%0.1f$, max=$%0.1f$, $\lambda$=$%d$'%(quant_min, quant_max, quant_level));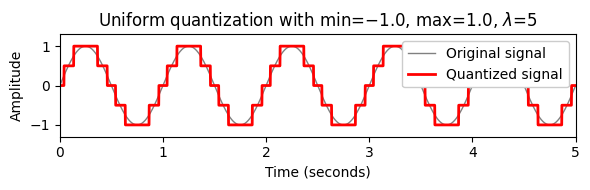
비균일(Nonuniform) 양자화
균일 양자화에서 양자화 수준은 등거리(equidistant) 방식으로 배치(spaced)된다. 그렇지 않은 경우 비균일(nonuniform) 양자화라고 한다. 예를 들어 오디오 신호의 경우 로그 방식으로 간격을 둔 양자화 수준을 선택하는 경우가 많다. 소리 강도에 대한 인간의 인식이 본질적으로 대수적이기 때문이다.
따라서 인지적 관점에서 보면 높은 진폭 값을 인코딩하는 것보다 낮은 진폭 값을 인코딩하는 데 더 많은 비트를 활용하는 것이 유리할 수 있다(낮은 진폭 값에서 인간은 소리 강도의 변화에 더 민감함).
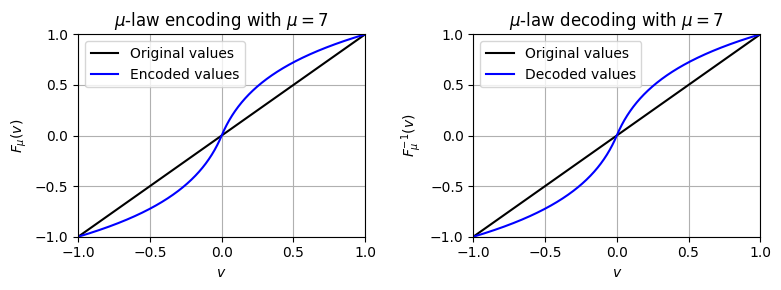
로그 양자화에 대한 한 가지 접근 방식으로 다음과 같이 정의되는 \(\mu\)-law 인코딩이 있다. \[F_\mu(v) = \mathrm{sgn}(v) \frac{\ln(1+ \mu |v|)}{\ln(1+\mu)}\] for values \(v\in[-1,1]\), where \(\mathrm{sgn}\) denotes the signum function
파라미터 \(\mu\in\mathbb{R}_{>0}\)는 적용되는 compression 정도를 결정하는 정수이다.
실제로는 비균일 \(8\)비트 양자화 체계를 도출하기 위해 \(\mu=255\)를 자주 사용한다. 인코딩 \(F_\mu\)는 strictly 증가 단조 함수로, \([-1,1]\) 간격을 낮은 값은 확장되고 높은 값은 압축되도록 자기 자체에 매핑한다.
그 역인 \(\mu\)-law 디코딩(decoding) 은 다음과 같다. \[F_\mu^{-1}(v) = \mathrm{sgn}(v) \frac{(1 + \mu)^{|v|}- 1}{\mu}\] for values \(v\in[-1,1]\)
다음 코드 셀에서 \(F_\mu\) 함수와 그 역 \(F_\mu^{-1}\)를 구현하고 다른 파라미터 \(\mu\)에 대한 결과를 설명한다.
def encoding_mu_law(v, mu=255.0):
"""mu-law encoding
Args:
v (float): Value between -1 and 1
mu (float): Encoding parameter (Default value = 255.0)
Returns:
v_encode (float): Encoded value
"""
v_encode = np.sign(v) * (np.log(1.0 + mu * np.abs(v)) / np.log(1.0 + mu))
return v_encode
def decoding_mu_law(v, mu=255.0):
"""mu-law decoding
Args:
v (float): Value between -1 and 1
mu (float): Dencoding parameter (Default value = 255.0)
Returns:
v_decode (float): Decoded value
"""
v_decode = np.sign(v) * (1.0 / mu) * ((1.0 + mu)**np.abs(v) - 1.0)
return v_decodedef plot_mu_law(mu=255.0, figsize=(8, 3)):
"""Helper function for plotting a signal and its quantized version
Args:
mu (float): Dencoding parameter (Default value = 255.0)
figsize (tuple): Figure size (Default value = (8.5, 2))
"""
values = np.linspace(-1, 1, 1000)
values_encoded = encoding_mu_law(values, mu=mu)
values_decoded = encoding_mu_law(values, mu=mu)
plt.figure(figsize=figsize)
ax = plt.subplot(1, 2, 1)
ax.plot(values, values, color='k', label='Original values')
ax.plot(values, values_encoded, color='b', label='Encoded values')
ax.set_title(r'$\mu$-law encoding with $\mu=%.0f$' % mu)
ax.set_xlabel('$v$')
ax.set_ylabel(r'$F_\mu(v)$')
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.grid('on')
ax.legend()
ax = plt.subplot(1, 2, 2)
ax.plot(values, values, color='k', label='Original values')
ax.plot(values, values_decoded, color='b', label='Decoded values')
ax.set_title(r'$\mu$-law decoding with $\mu=%.0f$' % mu)
ax.set_xlabel('$v$')
ax.set_ylabel(r'$F_\mu^{-1}(v)$')
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.grid('on')
ax.legend()
plt.tight_layout()
plt.show()plot_mu_law(mu=255.0)
plot_mu_law(mu=7.0)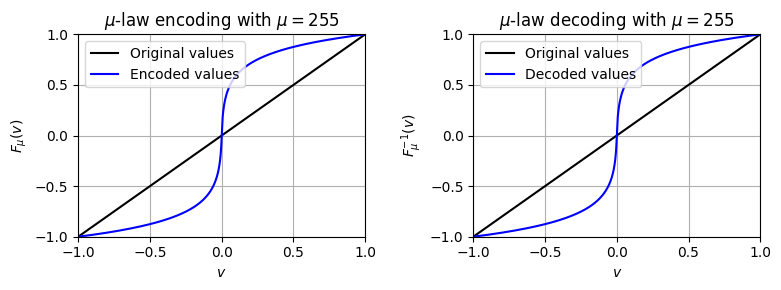
비균일 양자화 구현
- 먼저 주어진 신호를 \(F_\mu\)를 사용하여 인코딩한 다음, 균일 양자화를 적용하고, 마지막으로 \(F_\mu^{-1}\)를 사용하여 양자화된 신호를 디코딩해보자. 다음 코드에서 신호 샘플을 \([-1,1]\) 범위에 있는 경우로 제한한다. 뒤의 그림은 위의 정현파 예제 형식을 따르는 균일 양자화와 비균일 양자화의 차이를 보여준다.
def quantize_nonuniform_mu(x, mu=255.0, quant_level=256):
"""Nonuniform quantization approach using mu-encoding
Args:
x (np.ndarray): Original signal
mu (float): Encoding parameter (Default value = 255.0)
quant_level (int): Number of quantization levels (Default value = 256)
Returns:
x_quant (np.ndarray): Quantized signal
"""
x_en = encoding_mu_law(x, mu=mu)
x_en_quant = quantize_uniform(x_en, quant_min=-1, quant_max=1, quant_level=quant_level)
x_quant = decoding_mu_law(x_en_quant, mu=mu)
return x_quantdur = 5
x, t = generate_sinusoid(dur=dur, Fs=1000, amp=1, freq=1, phase=0.0)
quant_level = 8
x_quant = quantize_uniform(x, quant_min=-1, quant_max=1, quant_level=quant_level)
plot_signal_quant(x, t, x_quant, xlim=[0, dur], ylim=[-1.3,1.3],
title=r'Uniform quantization with $\lambda$=$%d$'%(quant_level));
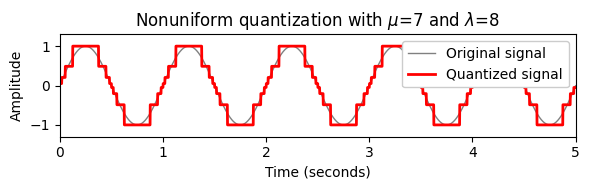
mu = 7
x_quant = quantize_nonuniform_mu(x, mu=mu, quant_level=quant_level)
plot_signal_quant(x, t, x_quant, xlim=[0, dur], ylim=[-1.3,1.3],
title=r'Nonuniform quantization with $\mu$=$%d$ and $\lambda$=$%d$'%(mu, quant_level));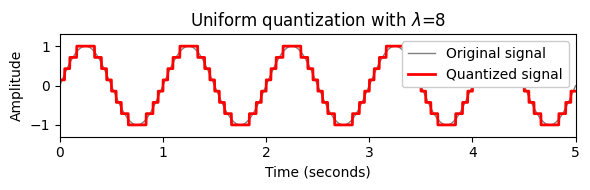
- 위의 접근 방식은 두 개의 파라미터, \(\mu\)(인코딩 파라미타) 및 \(\lambda\)(간격 \([-1,1]\)의 양자화 레벨 수)에 따라 달라지는 비균일 양자화 함수를 생성한다. 다음 코드 셀에서는 다양한 파라미터 설정에 대한 양자화 오류(quantization error)와 양자화 함수의 그래프를 보여준다. 양자화 오류는 \(|v|\approx 1\)인 \(v\) 값보다 \(|v|\approx 0\)인 \(v\) 값에서 훨씬 더 낮다.
plt.figure(figsize=(12,3))
ax = plt.subplot(1, 3, 1)
plot_graph_quant_function(ax, mu=3, quant_level=4, quant='nonuniform')
ax = plt.subplot(1, 3, 2)
plot_graph_quant_function(ax, mu=7, quant_level=8, quant='nonuniform')
ax = plt.subplot(1, 3, 3)
plot_graph_quant_function(ax, mu=15, quant_level=16, quant='nonuniform')
plt.tight_layout()
plt.show()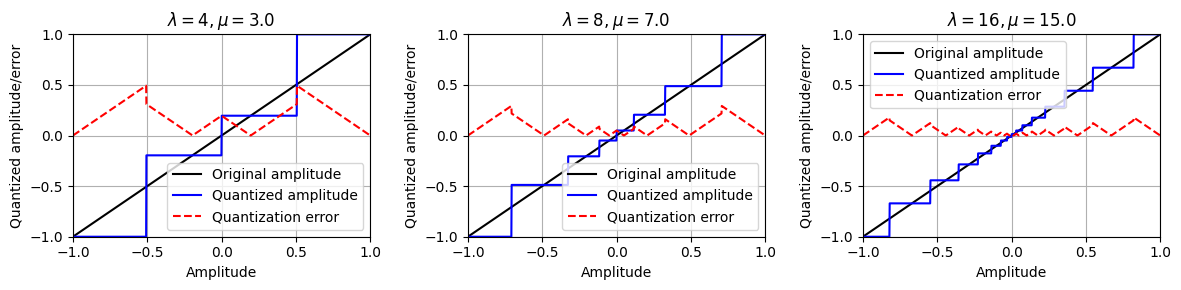
양자화 잡음 (Quantization Noise)
- 신호의 양자화는 손실이 많은 작업이다. 이 과정에서 발생하는 왜곡을 양자화 잡음이라고 한다. 다음 코드 셀에서 샘플 값을 인코딩하기 위해 다른 수의 비트를 사용하여 C 장음계의 피아노 녹음을 양자화하여 이러한 왜곡의 impression을 줘본다. \(b\in\mathbb{N}\) 비트를 사용하여 \(2^b\)의 서로 다른 양자화 레벨을 인코딩할 수 있다.
def display_signal_quant(x, Fs, number_of_bits):
quant_level = 2 ** number_of_bits
x_quant = quantize_uniform(x, quant_min=-1, quant_max=1, quant_level=quant_level)
print('Signal after uniform quantization (%d bits) :'%number_of_bits, flush=True)
ipd.display(ipd.Audio(x_quant, rate=Fs))
return x_quantx, Fs = librosa.load("../audio/piano_c_scale.wav", sr=11025)
print('Original audio signal (16 bits):', flush=True)
ipd.display(ipd.Audio(x, rate=Fs) )
x_quant = display_signal_quant(x=x, Fs=Fs, number_of_bits=8)
x_quant = display_signal_quant(x=x, Fs=Fs, number_of_bits=4)
x_quant = display_signal_quant(x=x, Fs=Fs, number_of_bits=2)Original audio signal (16 bits):Signal after uniform quantization (8 bits) :Signal after uniform quantization (4 bits) :Signal after uniform quantization (2 bits) :균일 및 비균일 양자화에 대한 양자화 노이즈
- 위의 C 메이저 스케일의 피아노 녹음을 사용하여 양자화 노이즈 결과 균일 및 비균일 양자화를 비교한다. 샘플 값을 인코딩하기 위해 서로 다른 비트 수를 고려한다. 특히, \(8\) 비트 균일 양자화를 사용할 때보다 \(8\) 비트 비균일 양자화를 사용할 때 더 낮은 노이즈 레벨을 인지한다.
def compare_quant_signal(x, Fs, number_of_bits):
quant_level = 2 ** number_of_bits
mu = quant_level-1
x_qu = quantize_uniform(x, quant_min=-1, quant_max=1, quant_level=quant_level)
x_qn = quantize_nonuniform_mu(x, mu=mu, quant_level=quant_level)
audio_player_list([x, x_qu, x_qn], [Fs, Fs, Fs], width=160,
columns=['Original (16 bits)', 'Uniform (%d bits)'%number_of_bits, 'Nonuniform (%d bits)'%number_of_bits])x, Fs = librosa.load("../audio/piano_c_scale.wav", sr=11025)
compare_quant_signal(x, Fs, number_of_bits=8)
compare_quant_signal(x, Fs, number_of_bits=4)
compare_quant_signal(x, Fs, number_of_bits=2)| Original (16 bits) | Uniform (8 bits) | Nonuniform (8 bits) |
|---|---|---|
| Original (16 bits) | Uniform (4 bits) | Nonuniform (4 bits) |
|---|---|---|
| Original (16 bits) | Uniform (2 bits) | Nonuniform (2 bits) |
|---|---|---|
간섭 및 비팅 (Interference and Beating)
간섭(Interference)
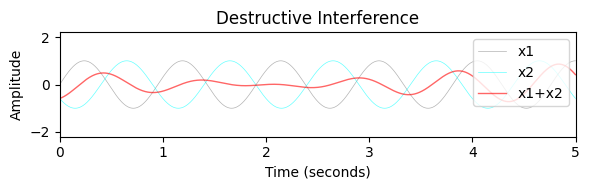
- 신호 처리에서 간섭(interference)은 한 파동이 비슷한 주파수의 다른 파동과 중첩(superimposed)될 때 발생한다. 한 파동의 파고(crest)가 어떤 지점에서 다른 파동의 파고와 만나면 일정 기간 동안 개별적 크기가 합산되며 이를 보강 간섭(constructive interference)이라고 한다. 반대로, 한 파동의 파고가 다른 파동의 파고와 만나면 크기가 일정 시간 동안 상쇄되는데, 이를 상쇄 간섭(destructive interference)이라고 한다.
def plot_interference(x1, x2, t, figsize=(6, 2), xlim=None, ylim=None, title=''):
"""Helper function for plotting two signals and its superposition
Args:
x1: Signal 1
x2: Signal 2
t: Time
figsize: figure size (Default value = (8, 2))
xlim: x limits (Default value = None)
ylim: y limits (Default value = None)
title: figure title (Default value = '')
"""
plt.figure(figsize=figsize)
plt.plot(t, x1, color='gray', linewidth=.5, linestyle='-', label='x1', alpha=.6)
plt.plot(t, x2, color='cyan', linewidth=.5, linestyle='-', label='x2', alpha=.6)
plt.plot(t, x1+x2, color='red', linewidth=1.0, linestyle='-', label='x1+x2', alpha=.6)
if xlim is None:
plt.xlim([0, t[-1]])
else:
plt.xlim(xlim)
if ylim is not None:
plt.ylim(ylim)
plt.xlabel('Time (seconds)')
plt.ylabel('Amplitude')
plt.title(title)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()dur = 5
x1, t = generate_sinusoid(dur=dur, Fs=1000, amp=1, freq=1.05, phase=0.0)
x2, t = generate_sinusoid(dur=dur, Fs=1000, amp=1, freq=0.95, phase=0.8)
plot_interference(x1, x2, t, xlim=[0, dur], ylim=[-2.2,2.2], title='Constructive Interference');
dur = 5
x1, t = generate_sinusoid(dur=dur, Fs=1000, amp=1, freq=1.05, phase=0.0)
x2, t = generate_sinusoid(dur=dur, Fs=1000, amp=1, freq=1.00, phase=0.4)
plot_interference(x1, x2, t, xlim=[0, dur], ylim=[-2.2,2.2], title='Destructive Interference');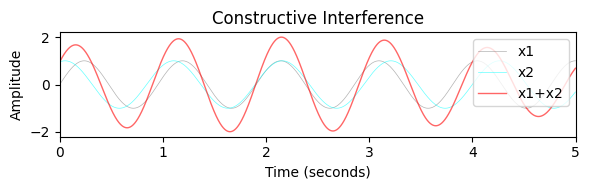
비팅(Beating)
앞의 그림은 주파수가 비슷한 두 정현파가 더해지거나(보강 간섭) 상쇄(상쇄 간섭)될 수 있음을 보여주었다.
\(f_1(t)=\sin(2\pi \omega_1 t)\) 및 \(f_2(t)=\sin(2\pi \omega_2 t)\)를 뚜렷하지만 가까운 주파수 \(\omega_1\approx\omega_2\)의 두 정현파라고 하자.
이제 이 두 정현파의 중첩 \(f_1+f_2\)가 진폭이 천천히 변하는 단일 사인파처럼 보이는 함수를 생성한다는 것을 볼 수 있다. 이 현상은 비팅(beating) 이라고 한다. 수학적으로 이 현상은 삼각 항등식 (trigonometric identity)의 결과이다. \[\sin(2\pi \omega_1t)+\sin(2\pi \omega_2t)= 2\cos\left(2\pi\frac{\omega_1-\omega_2}{2}t\right)\sin\left(2\pi\frac{\omega_1+\omega_2}{2}t\right).\]
\(\omega_1-\omega_2\)의 차이가 작으면 코사인 항은 사인 항에 비해 빈도가 낮다.
결과적으로 신호 \(f_1+f_2\)는 주파수 \(|\omega_1-\omega_2|\)의 천천히 변하는 진폭 포락선(amplitude envelope)을 가지는 주파수 \((\omega_1+\omega_2)/2\)의 사인파로 볼 수 있다.
이 비율은 코사인 항의 빈도 \((\omega_1-\omega_2)/2\)의 두 배이다.
Fs = 4000
dur = 5
x1, t = generate_sinusoid(dur=dur, Fs=Fs, amp=0.5, freq=200)
x2, t = generate_sinusoid(dur=dur, Fs=Fs, amp=0.5, freq=203)
plot_interference(x1, x2, t, ylim=[-1.1,1.1], xlim=[0, dur],
title=r'Beating with beating frequency $|\omega_1-\omega_2|=3$ ($\omega_1=200, \omega_2=203$)');
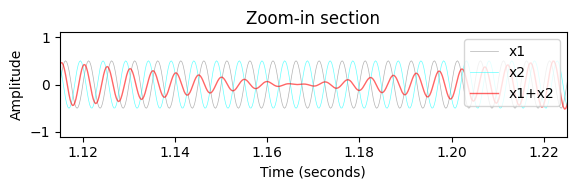
plot_interference(x1, x2, t, ylim=[-1.1,1.1], xlim=[1.115, 1.225], title=r'Zoom-in section');
ipd.display(ipd.Audio(x1+x2, rate=Fs))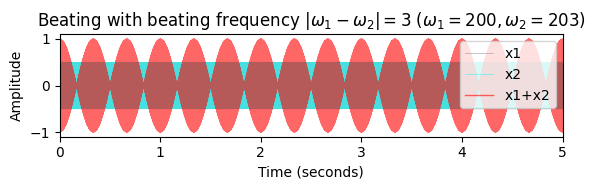
처프(Chirp) 실험
- 비팅(beating)효과를 설명하기 위해 처프 신호(시간에 따라 주파수가 증가)를 보자.
- \(\omega_0,\omega_1\in\mathbb{R}\)를 두 주파수 파라미터(헤르츠 단위)라고 하고, \(T\in\mathbb{R}\)를 듀레이션 파라미터(초단위)라고 하자.
- \(\omega_0\)에서 시작하여 \(\omega_1\)로 주파수가 선형적으로 증가하는 듀레이션 \(d\)의 선형 처프는 다음과 같이 계산된다.
- $ f(t)=( t^2 + 2_0t)$ for \(t\in[0,T]\)
- 시간 \(t\)에서 처프 신호 \(f\)의 순간 주파수 (instantaneous frequency) 는 정현파의 인수를 \(2\pi\)로 나눈 것의 도함수로 주어진다.
\[ g(t) = \frac{\omega_1-\omega_0}{T} t + \omega_0. \]
주파수 \(\omega_0=220.0~\mathrm{Hz}\)(피치 \(\mathrm{A3}\))에서 시작하여 주파수 \(\omega_1=311.1~\mathrm{Hz}\)(피치 \(\mathrm{E}^\flat 4\))로 끝나는 듀레이션 \(T=20~\mathrm{sec}\)의 선형 처프 신호를 보자.
또한 동일한 듀레이션의 주파수 \(261.5~\mathrm{Hz}\)(피치 \(\mathrm{C4}\))를 갖는 정현파를 생각해보자.
이 신호의 중첩을 들을 때, 처음에는 \(\mathrm{A3}\) 및 \(\mathrm{C4}\) 두 개의 개별 피치를 인식한다.
처프가 \(\mathrm{C4}\)에 가까워지면 두 음이 하나의 소리로 합쳐지기 시작한다. 동시에 처음에는 속도가 느려졌다가 사라지고(처프가 \(\mathrm{C4}\)에 도달하면), 다시 속도가 빨라지는 비팅 효과를 볼 수 있다. 마지막에 다시 \(\mathrm{E}^\flat 4\) 및 \(\mathrm{C4}\)인 두 피치를 인식한다.
def generate_chirp_linear(dur, freq_start, freq_end, amp=1.0, Fs=22050):
"""Generation chirp with linear frequency increase
Args:
dur (float): Duration (seconds) of the signal
freq_start (float): Start frequency of the chirp
freq_end (float): End frequency of the chirp
amp (float): Amplitude of chirp (Default value = 1.0)
Fs (scalar): Sampling rate (Default value = 22050)
Returns:
x (np.ndarray): Generated chirp signal
t (np.ndarray): Time axis (in seconds)
freq (np.ndarray): Instant frequency (in Hz)
"""
N = int(dur * Fs)
t = np.arange(N) / Fs
a = (freq_end - freq_start) / dur
freq = a * t + freq_start
x = amp * np.sin(np.pi * a * t ** 2 + 2 * np.pi * freq_start * t)
return x, t, freqf_pitch = lambda p: 440 * 2 ** ((p - 69) / 12)
Fs = 4000
dur = 20
freq_start = f_pitch(57) # A3
freq_end = f_pitch(63) # Eflatp4
freq_sin = f_pitch(60) # C4
x1, t, freq = generate_chirp_linear(dur=dur, freq_start=freq_start, freq_end=freq_end, amp=0.5, Fs=Fs)
x2, t = generate_sinusoid(dur=dur, Fs=Fs, amp=0.5, freq=freq_sin)
y = x1 + x2
ipd.display(ipd.Audio(y, rate=Fs))
plot_interference(x1, x2, t, xlim=[0, dur], ylim=[-1.1,1.1],
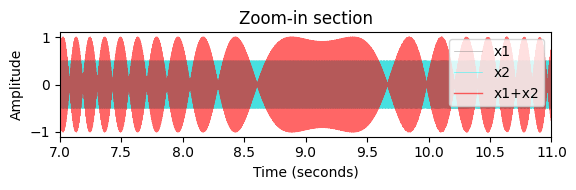
title=r'Superposition of a linear chirp $x_1$ (A3 to E$^\flat$4) and sinusoid $x_2$ (C4)');
plot_interference(x1, x2, t, xlim=[7, 11], ylim=[-1.1,1.1], title='Zoom-in section');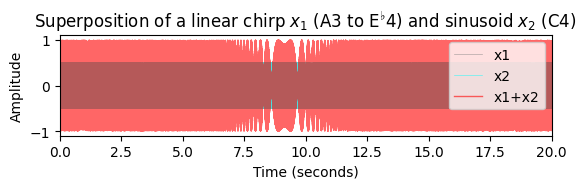
출처:
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C2/C2.html
\(\leftarrow\) 3.4. 단기 푸리에 변환 (STFT) (2)